Heap Sort
Implement a function that performs a heap sort. The function should take in an array of integers and return an array with the integers sorted in ascending order. The input array is modified in-place.
Examples
heapSort([9, 3, 6, 2, 1, 11]); // [1, 2, 3, 6, 9, 11]heapSort([12, 16, 14, 1, 2, 3]); // [1, 2, 3, 12, 14, 16]
Recap
Heap sort is a comparison-based sorting algorithm that iteratively builds the unsorted array into a max heap data structure to identify the max element, and progressively swaps it to the end of the unsorted array to build a sorted array.
Max Heaps
To understand heap sort, we need to first understand the heap data structure:
- A binary heap is a partially ordered, complete binary tree which satisfies a heap property, similar to binary search trees, but with different ordering.
- Heap property = Specific relationship between the parent and child nodes which specifies their order. One example is the max heap property, which specifies that all parent nodes have to >= than their child nodes. The order between child nodes on the same level does not matter. Hence, the largest nodes are always on the top, and the smallest nodes are at the bottom. Nodes on the same level are unordered:
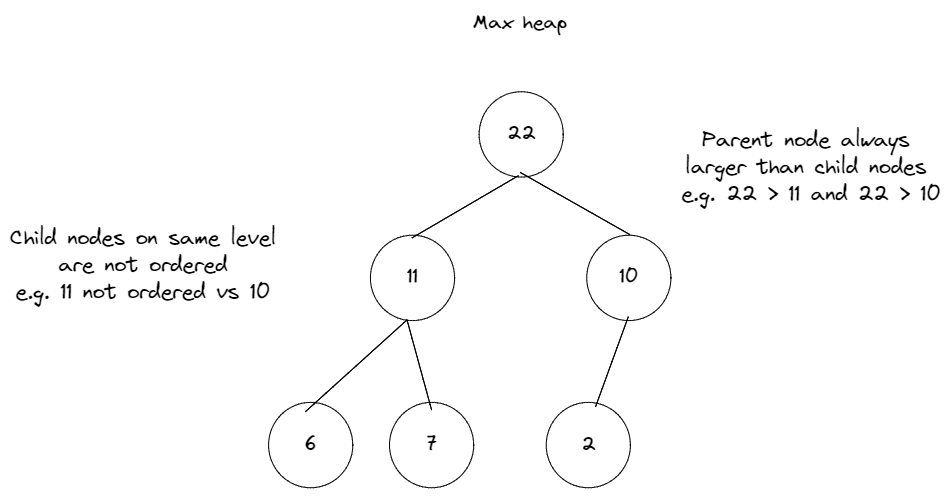
- Complete binary tree = All levels of the tree are completely filled. If the last level is partially filled, it is filled first from left to right.
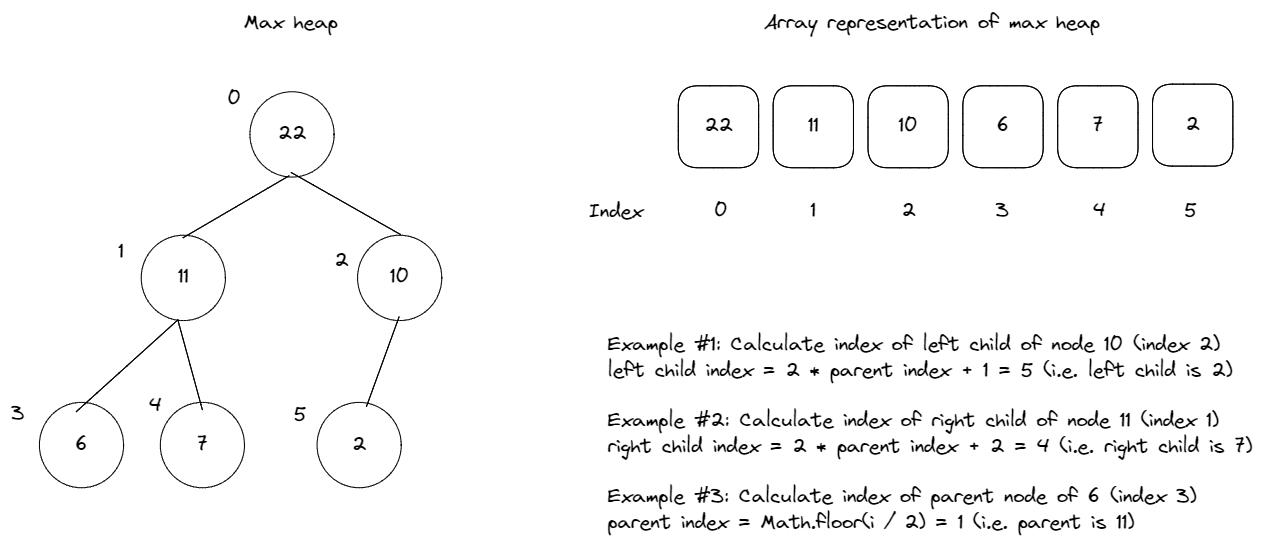
- Heaps are frequently implemented as arrays. We can use the following formula to compute the parent, left child and right child's indexes within the array representation of a heap:
- Left child idx = 2 * parentIdx + 1
- Right child idx = 2 * parentIdx + 2
How Heap Sort Works
A heap sort essentially works by the following steps:
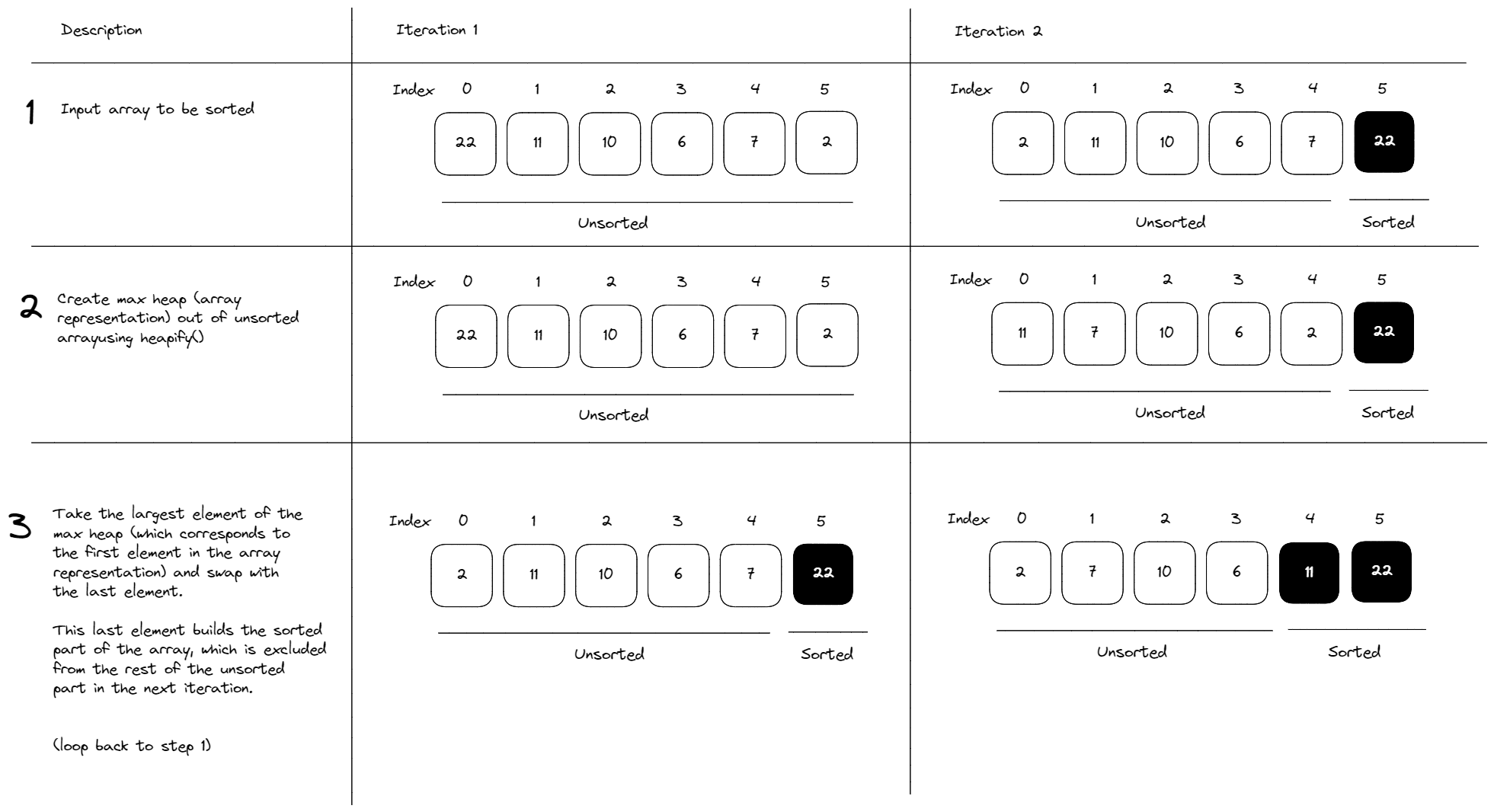
Heap Sort (Official solution)
Heap sort is an in-place, comparison-based algorithm that works well for large sized arrays since it has a time complexity of O(nlog(n)).
It also does not require any additional memory space to sort the data as it is an in-place sorting algorithm. However, it is not a stable sort, which means that the order of elements with equal values may not be preserved.
Clarification questions
If unspecified:
- Should the data be sorted in an ascending or descending order?
- Should the data be sorted in-place or is it acceptable to use additional data structures?
- What kinds of inputs do we need to handle?
- Will it just be an array of integers or should we handle other data types?
- Are there a large number of duplicate elements?
- How should negative numbers be handled?
Solution
Note: This question tackles in-place sorting for an output in ascending order. Refer to the 'Notes' section below on how to handle other cases.
/*** @param {Array<number>} arr The input integer array to be sorted.* @return {Array<number>}*/export default function heapSort(arr) {// Begin by building a max heap.const size = arr.length;for (let i = Math.floor(size / 2 - 1); i >= 0; i--) {// Start with the index of the last parent node.// heapify: Swaps parent with child as long as child is larger than parent.heapify(arr, size, i);}// Iterate through the heap backwards, swapping the last element of the heap with the max element (the root of a max heap).// Max elements swapped to the end constitute the sorted part of the array (ignored in the next iteration by "i--").for (let i = size - 1; i >= 0; i--) {[arr[0], arr[i]] = [arr[i], arr[0]];// Build a max heap again in preparation for the swap in the next iteration.heapify(arr, i, 0);}return arr;}function heapify(arr, size, parentIdx) {let largest = parentIdx; // Initiate largest value's index with parent index.const leftChildIdx = 2 * parentIdx + 1; // Calculate index of left child.const rightChildIdx = 2 * parentIdx + 2; // Calculate index of right child.// Set `largest` to index with highest value between parent, left and right child.// See if left child of parent exists and is larger than parent.if (leftChildIdx < size && arr[leftChildIdx] > arr[largest]) {largest = leftChildIdx;}// See if right child of parent exists and is larger than parent.if (rightChildIdx < size && arr[rightChildIdx] > arr[largest]) {largest = rightChildIdx;}// If `largest` is not the current parent, swap positions with the current parent.if (largest !== parentIdx) {[arr[parentIdx], arr[largest]] = [arr[largest], arr[parentIdx]];// Continue to recursively heapify the affected subtree.heapify(arr, size, largest);}}
Edge cases
- Non-integer element input: If the input array comprises of elements of different data types, you may need to return an error, settle for sorting on a best-effort basis, for e.g., only sorting a subset of the input data, or even define custom comparison functions for non-integers.
- Single element / Empty input: Either return the original data structure, raise an error, or clarify required handling.
- Already sorted input: You may want to detect sorting and return the input unchanged.
- Invalid input: If the input is not an array, consider throwing an error.
Notes
- If asked to sort in descending order: Change comparison operators in
heapify()function in order to build a min heap instead of a max heap, then use it as per normal inheapSort:
function heapifyMin(arr, size, parentIdx) {let smallest = parentIdx; // initiate smallest value's index with parent indexconst leftChildIdx = 2 * parentIdx + 1; // calculate index of left childconst rightChildIdx = 2 * parentIdx + 2; // calculate index of right child// set 'smallest' to index with lowest value between parent, left and right childif (leftChildIdx < size && arr[leftChildIdx] < arr[smallest]) {smallest = leftChildIdx;}if (rightChildIdx < size && arr[rightChildIdx] < arr[smallest]) {smallest = rightChildIdx;}// if 'smallest' is not the current parent, swap positions with the current parentif (smallest !== parentIdx) {[arr[parentIdx], arr[smallest]] = [arr[smallest], arr[parentIdx]];// continue to recursively heapify the affected subtreeheapifyMin(arr, size, smallest);}}
- If asked to use additional data structures or to write a pure function rather than sorting the data in-place, create a copy of the array and return a shallow copy of the sorted array:
function heapSort(arr) {const result = arr.slice(0);const size = arr.length;for (let i = Math.floor(size / 2 - 1); i >= 0; i--) {heapify(result, size, i);}for (let i = size - 1; i >= 0; i--) {[result[0], result[i]] = [result[i], result[0]];heapify(result, i, 0);}return result;}
- If you're wondering why
Math.floor(size / 2 - 1)was able to calculate the index of the last parent node, it's because in a complete binary tree, the number of parent nodes is equal to Math.floor(size / 2). The -1 at the end is needed because the indices in the array start at 0, not 1.
Big-O analysis
Let's analyze the algorithm's time and space complexity.
Time complexity
The best, average and worst case time complexity of heap sort is O(nlog n). Regardless of whether the elements are already sorted, the algorithm will always take O(nlog(n)) time to complete. This is accurate unless you detect sorted arrays and return them immediately for a O(n) time complexity at the best case with a completely sorted array.
To understand the time complexity of heap sort, understanding the time complexity of heapify() is critical. In heapify(), we walk through the tree from top to bottom, which means the time complexity is proportional to the height of the binary tree, which is O(log(n)) at most for a tree of size n. Therefore, time complexity for the heapify() function is O(log(n)).
The time complexity of heap sort is O(nlog(n)) as there are 2 steps to the algorithm: Building the heap and then sorting the data.
- Building the heap has a time complexity of O(n) because the
heapify()method is called for each parent node backward, starting with the last node and ending at the tree root. On average, this can be done optimally at O(n). - When sorting the data, we call the
heapify()method n-1 times to maintain the heap property on the unsorted part of the array. Hence, the total time complexity is O(nlog(n)).
The total time complexity of heap sort is the sum of the time complexity of each step, which is O(n) + O(nlog(n)) = O(nlog(n)).
Space complexity
The space complexity for heap sort is O(1), as it does in-place sorting and does not require additional storage proportional to input size.
However, the space complexity will be O(n) if the algorithm is implemented using recursive function calls, which requires additional memory space to store the function call stack.
You must be signed in to view your submissions
Loading editor
Loading editor
Loading tests
JavaScript Console
console.log() statements will appear here.