Dijkstra's Algorithm
Given a weighted directed graph represented as an adjacency list (graph) and a starting node (source), implement Dijkstra's algorithm to find the shortest path distances from source to all other nodes in the graph. The graph contains nodes and weighted edges.
Input
graph: An object representing the adjacency list of the graph. Each key is a node identifier (e.g.'A','B'), and its value is another object that maps each neighboring node to the non-negative weight of the edge connecting them.source: The identifier of the starting node from which to calculate shortest paths.
Output
- An object where keys are node identifiers and values represent the shortest distance from
sourceto that node. Nodes that are unreachable fromsourceshould have their distance set toInfinity(use the built-inInfinityconstant).
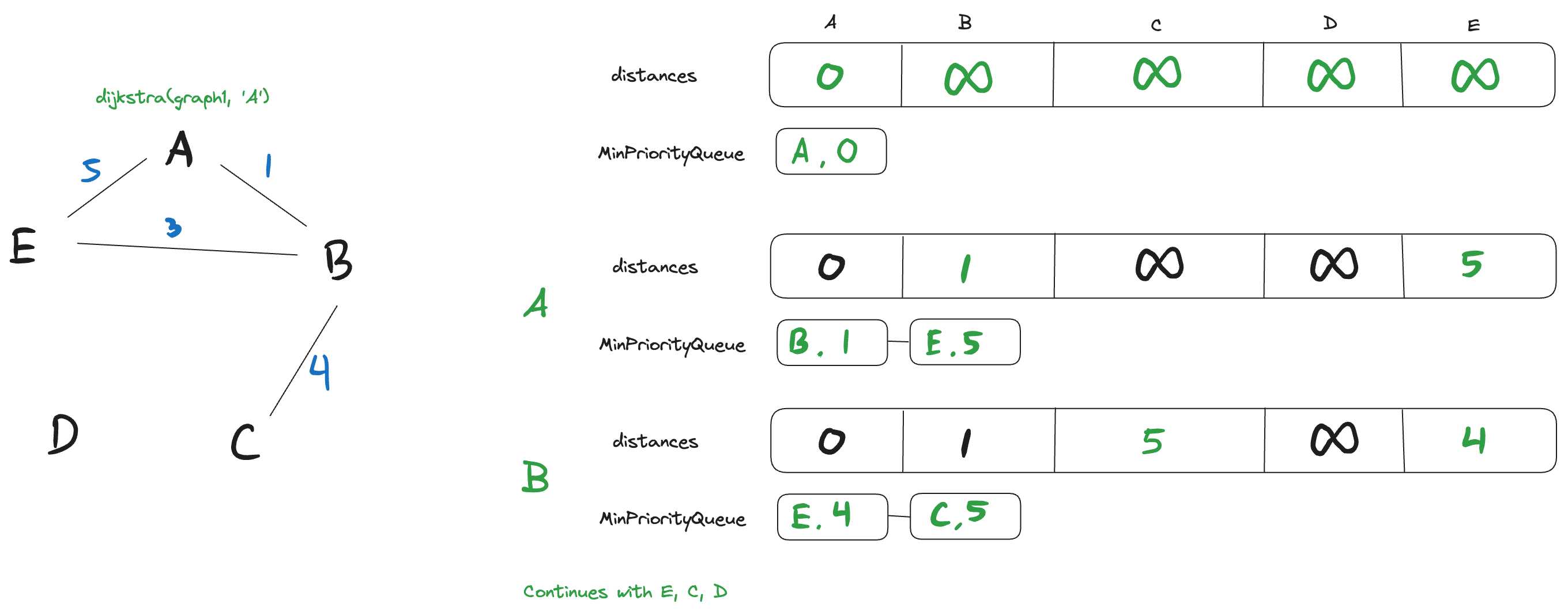
Examples
const graph1 = {A: { B: 1, C: 4 },B: { E: 3, F: 2 },C: { G: 2 },D: { C: 3, J: 5 },E: { D: 2 },F: {},G: { H: 1 },H: { F: 4, J: 3 },I: {},J: {},};dijkstra(graph1, 'A'); // Returns distances: { A: 0, B: 1, C: 4, D: 6, E: 4, F: 3, G: 6, H: 7, I: Infinity, J: 10 }const graph2 = {A: { B: 2, C: 5 },B: { D: 1, E: 4 },C: { F: 3, G: 2 },D: {},E: {},F: {},G: {},};dijkstra(graph2, 'A'); // Returns distances: { A: 0, B: 2, C: 5, D: 3, E: 6, F: 8, G: 7 }
Constraints
- 1 <= Number of nodes <= 1000
- 0 <= Edge weight <= 10000
- The graph may contain cycles
- The graph may be disconnected
Recap (Hint)
Dijkstra's algorithm is a basic algorithm used to find the shortest path between nodes in a weighted graph. This algorithm can handle graphs with non-negative weights and is commonly used in routing and as a subroutine in other graph algorithms. Here are some typical use cases:
- In GPS systems to find the shortest driving route between locations.
- In network routing algorithms to find the shortest path for data packets.
- In scheduling theory to find the shortest (least time-consuming) path through a series of tasks.
- Generating a minimum spanning tree (MST) of a weighted graph.
Here's how Dijkstra's algorithm works:
- Start with a set of all nodes in the graph, and assign them a tentative distance value: zero for the initial node, and infinity for all other nodes. Set the initial node as the current node.
- For the current node, consider all of its unvisited neighbors and calculate their tentative distances. Compare the newly calculated tentative distance to the current assigned value and assign the smaller one.
- Once we have considered all the unvisited neighbors of the current node, mark the current node as visited. A visited node will not be checked again.
- If the destination node has been marked visited or if the smallest tentative distance among the nodes in the unvisited set is infinity (occurs when there is no connection between the initial node and remaining unvisited nodes), then stop. The algorithm has finished.
- Otherwise, select the unvisited node that is marked with the smallest tentative distance, set it as the new "current node," and go back to step 2.
- The result is a map of the shortest distances from the initial node to all other nodes.
Dijkstra's Algorithm (Official solution)
Reasoning
Dijkstra’s algorithm computes the shortest paths from a source node in a graph with non-negative edge weights. It uses a greedy approach: at each step, it selects the unvisited node with the smallest known distance. A min-heap efficiently performs this selection. When a shorter path to a neighbor is found, the algorithm updates its distance (relaxation) and pushes it into the heap. This strategy guarantees correctness because all edge weights are non-negative.
Dijkstra's algorithm assumes non-negative weights. For graphs with negative weights, other algorithms like Bellman-Ford are needed.
Algorithm
The provided solution implements Dijkstra's algorithm using a priority queue (min-heap) for efficiency.
- Initialization: Start with distances to all nodes set to infinity, except the source node which is set to zero.
- Priority queue: Use a priority queue to greedily select the next node with the smallest known distance.
- Relaxation: For each selected node, update the shortest distance to its neighboring nodes if a shorter path is found via the current node. Subsequently add or or update that neighbor's distance in the priority queue.
- Termination: The algorithm terminates when the priority queue is empty, indicating all reachable nodes have been processed.
/*** MinHeap: A minimum heap implementation to serve as a priority queue.* Each heap element is an object of the form { vertex, weight }.*/class MinHeap {constructor() {this.heap = [];this.position = {}; // Maps each vertex to its index in the heap.}// Helper method to swap two elements and update their positions.swap(i, j) {[this.heap[i], this.heap[j]] = [this.heap[j], this.heap[i]];this.position[this.heap[i].vertex] = i;this.position[this.heap[j].vertex] = j;}// Bubbles up the element at index i to restore heap property.percolateUp(i) {while (i > 0) {const parent = Math.floor((i - 1) / 2);if (this.heap[parent].weight > this.heap[i].weight) {this.swap(i, parent);i = parent;} else {break;}}}// Bubbles down the element at index i to restore heap property.percolateDown(i) {const n = this.heap.length;while (true) {const left = 2 * i + 1;const right = 2 * i + 2;let smallest = i;if (left < n && this.heap[left].weight < this.heap[smallest].weight) {smallest = left;}if (right < n && this.heap[right].weight < this.heap[smallest].weight) {smallest = right;}if (smallest !== i) {this.swap(i, smallest);i = smallest;} else {break;}}}/*** Inserts a new item into the heap or updates it if it already exists.* @param {{vertex: string, weight: number}} item The item to insert or update.*/insert(item) {// If the vertex exists, perform a decrease-key operation.if (this.position.hasOwnProperty(item.vertex)) {const i = this.position[item.vertex];if (item.weight < this.heap[i].weight) {this.heap[i].weight = item.weight;this.percolateUp(i);}return;}// Otherwise, add it as a new item.this.heap.push(item);const idx = this.heap.length - 1;this.position[item.vertex] = idx;this.percolateUp(idx);}/*** Removes and returns the minimum element (the root) from the heap.* @return {{vertex: string, weight: number}|undefined} The removed element.*/delete() {if (this.heap.length === 0) return undefined;const min = this.heap[0];const last = this.heap.pop();// Remove mapping for the vertex being removed.delete this.position[min.vertex];if (this.heap.length > 0) {this.heap[0] = last;this.position[last.vertex] = 0;this.percolateDown(0);}return min;}/*** Checks if the heap is empty.* @return {boolean} True if the heap is empty; otherwise, false.*/isEmpty() {return this.heap.length === 0;}/*** Returns the minimum element of the heap without removing it.* @return {{vertex: string, weight: number}|undefined}*/findMin() {return this.heap.length > 0 ? this.heap[0] : undefined;}}/*** Executes Dijkstra's algorithm to find the shortest paths from a source node* in a weighted graph.** @param {Record<string, Record<string, number>>} graph - The adjacency list representing the graph with weights.* @param {string} source - The source node from which to calculate shortest paths.* @return {Record<string, number>} - A dictionary where keys are node labels and values represent the shortest distances from the source node.*/export default function dijkstra(graph, source) {const distances = {};const minHeap = new MinHeap();// Initialize distances for every vertex.for (const vertex in graph) {// Set the source distance to 0 and all others to Infinity.distances[vertex] = vertex === source ? 0 : Infinity;// Insert the source with weight 0.// Optionally, we can insert only the source and then add vertices as needed.minHeap.insert({ vertex, weight: distances[vertex] });}const visited = new Set();while (!minHeap.isEmpty()) {// Extract the vertex with the smallest tentative distance.const { vertex: u, weight } = minHeap.delete();if (visited.has(u)) continue;visited.add(u);// For each neighbor of u, try to update its distance.for (const neighbor in graph[u]) {const newDist = distances[u] + graph[u][neighbor];if (newDist < distances[neighbor]) {distances[neighbor] = newDist;minHeap.insert({ vertex: neighbor, weight: newDist });}}}return distances;}
Edge cases
- Empty graphs: Return an empty dictionary or map without crashing
- Graphs with one or two nodes: Ensure that the algorithm can handle small graphs
- Graphs with non-connected components: Nodes not reachable from the source should have their distance remain as infinity
- Graphs with zero-weight edges: Confirm that zero-weight edges do not cause issues with the algorithm's logic
Big-O analysis
- Time complexity: O((V + E) log V). Using a min-heap, extracting the minimum takes O(log V) (done up to V times), and relaxing each of the E edges may also trigger a O(log V) heap update.
- Space complexity: O(v). Storing distances (
O(v)), the visited set (O(v)), and the priority queue (O(v)in the worst case).
You must be signed in to view your submissions
Loading editor
Loading editor
Loading tests
JavaScript Console
console.log() statements will appear here.