Breadth-first Search

JSTS

Write a function that implements the breadth-first search (BFS) algorithm on a directed graph (in adjacency list format), given a starting node.

BFS is an algorithm used for traversing a graph or a tree, starting from the root node and exploring all the neighbors at the current depth before moving on to nodes at the next depth level. The output from BFS is an array of the graph's nodes in the order they were traversed. Visiting neighboring nodes in any order is a valid BFS, but for this question, please visit each node's neighbors from left to right.

Examples

const graph1 = {
  A: ['B', 'C', 'D'],
  B: ['E', 'F'],
  C: ['G', 'H'],
  D: ['I', 'J'],
  E: ['D'],
  F: [],
  G: [],
  H: [],
  I: [],
  J: [],
};

breadthFirstSearch(graph1, 'A'); // ['A', 'B', 'C', 'D', 'E', 'F', 'G', 'H', 'I', 'J']

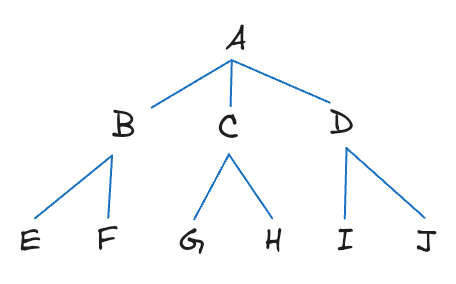
breadthFirstSearch(graph1, 'B'); // ['B', 'E', 'F', 'D', 'I', 'J']

const graph2 = {
  A: ['B', 'C'],
  B: ['D', 'E'],
  C: ['F', 'G'],
  D: [],
  E: [],
  F: [],
  G: [],
};

breadthFirstSearch(graph2, 'A'); // ['A', 'B', 'C', 'D', 'E', 'F', 'G']

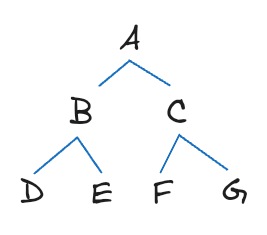
breadthFirstSearch(graph2, 'E'); // ['E']

A Queue data structure is also provided for you at the bottom of the skeleton code.

Recap (Hint)

Breadth-first search (BFS) is an algorithm used for traversing a graph or a tree. Here is an overview of how BFS works to traverse a graph, using the standard implementation that takes in an adjacency list (we use an array instead) and the root node:

Initialize a queue to store nodes to be visited. Enqueue the root node.
Initialize a set to track visited nodes.
Enter a loop that continues until the queue is empty. In each iteration of the loop:
1. Dequeue from the queue and mark it as visited.
2. Retrieve the neighbors of the node from the input graph.
3. For each neighbor, check if it has been visited. If it has not been visited, enqueue the node.
Return the set of visited nodes.

Breadth-first search is useful for the same purposes as Depth-first search, and it is especially useful for finding the shortest path between two nodes.

Coding and submission is not supported on mobile devices. Use a wider screen to practice solving this question within the editor.

Breadth-first Search

JSTS

Write a function that implements the breadth-first search (BFS) algorithm on a directed graph (in adjacency list format), given a starting node.

Examples

const graph1 = {
  A: ['B', 'C', 'D'],
  B: ['E', 'F'],
  C: ['G', 'H'],
  D: ['I', 'J'],
  E: ['D'],
  F: [],
  G: [],
  H: [],
  I: [],
  J: [],
};

breadthFirstSearch(graph1, 'A'); // ['A', 'B', 'C', 'D', 'E', 'F', 'G', 'H', 'I', 'J']

breadthFirstSearch(graph1, 'B'); // ['B', 'E', 'F', 'D', 'I', 'J']

const graph2 = {
  A: ['B', 'C'],
  B: ['D', 'E'],
  C: ['F', 'G'],
  D: [],
  E: [],
  F: [],
  G: [],
};

breadthFirstSearch(graph2, 'A'); // ['A', 'B', 'C', 'D', 'E', 'F', 'G']

breadthFirstSearch(graph2, 'E'); // ['E']

A Queue data structure is also provided for you at the bottom of the skeleton code.

Recap (Hint)

Initialize a queue to store nodes to be visited. Enqueue the root node.
Initialize a set to track visited nodes.
Enter a loop that continues until the queue is empty. In each iteration of the loop:
1. Dequeue from the queue and mark it as visited.
2. Retrieve the neighbors of the node from the input graph.
3. For each neighbor, check if it has been visited. If it has not been visited, enqueue the node.
Return the set of visited nodes.

Breadth-first search is useful for the same purposes as Depth-first search, and it is especially useful for finding the shortest path between two nodes.

Similar Questions

Depth-first Search

Clarification Questions

If unspecified:

Order of traversal: Should we use a standard pre-order traversal or other orders of traversal?
Input format: What is the format of the input data? Can we assume the input will be an adjacency list in the form of a JavaScript Object where keys are nodes and values are child nodes?
Output format: How should the output be formatted? Are there specific requirements or can we return an array with elements in the order of traversal?
Disconnected graphs: Do we have to consider or handle the case for disconnected graphs where there are multiple subgraphs that are not connected to each other?

Iterative solution

The solution implements the algorithm outlined in the description.

/**
 * @param {Record<string, Array<string>>} graph The adjacency list representing the graph.
 * @param {string} source The source node to start traversal from. Has to be a valid node if graph is non-empty.
 * @return {Array<string>} A BFS-traversed order of nodes.
 */
export default function breadthFirstSearch(graph, source) {
  // If there are no nodes in the graph, just return an empty array
  if (Object.keys(graph).length === 0) {
    return [];
  }

  // Create a queue to store the nodes to be visited.
  // Add the root node since we're doing a level-order BFS.
  const queue = new Queue();
  queue.enqueue(source);

  // Initialize a set that tracks visited nodes.
  const visited = new Set();

  // While there are nodes to visit.
  while (!queue.isEmpty()) {
    // Dequeue the node at the front of the queue.
    const node = queue.dequeue();

    // Mark the node as visited.
    visited.add(node);

    // Enqueue the neighbors of the current node.
    graph[node].forEach((neighbor) => {
      // Skip nodes that have already been visited.
      if (visited.has(neighbor)) {
        return;
      }

      queue.enqueue(neighbor);
    });
  }

  // The visited nodes is the traversal order.
  return Array.from(visited);
}

/*  Auxiliary classes */

/**
 * A Queue class with O(1) enqueue and dequeue is provided for you.
 * You can use it directly should you wish to.
 *
 * Example usage:
 * const q = new Queue();
 * q.enqueue('a');
 * q.enqueue('b');
 * q.dequeue(); //'a'
 * q.isEmpty(); // False
 */
class Node {
  constructor(value) {
    this.value = value;
    this.next = null;
  }
}

class Queue {
  constructor() {
    this.head = null;
    this.tail = null;
    this.length = 0;
  }

  isEmpty() {
    return this.length === 0;
  }

  enqueue(item) {
    const newNode = new Node(item);
    if (this.isEmpty()) {
      this.head = newNode;
    } else if (this.tail) {
      this.tail.next = newNode;
    }
    this.tail = newNode;
    this.length++;
  }

  dequeue() {
    if (this.isEmpty() || !this.head) {
      return null;
    } else {
      const removedNode = this.head;
      this.head = this.head.next;
      removedNode.next = null;
      this.length--;
      if (this.isEmpty()) {
        this.tail = null;
      }
      return removedNode.value;
    }
  }
}

Recursive solution

We can also perform BFS recursively, which is can be more intuitive in certain cases. The recursion call stack is an implicit stack to track which nodes to visit next.

/**
 * @param {Object} graph Node to array of neighboring nodes.
 * @param {string} source Source node to start traversal from. Has to be a valid node if graph is non-empty.
 * @return {Array<string>} A BFS-traversed order of nodes.
 */
export default function breadthFirstSearch(graph, source) {
  // If there are no nodes in the graph, just return an empty array
  if (Object.keys(graph).length === 0) {
    return [];
  }

  // Initialize a queue to keep track of nodes to visit.
  const queue = new Queue();
  const visited = new Set();

  // Add the source node to the queue and mark it as visited.
  queue.enqueue(source);
  visited.add(source);

  function traverse() {
    // If the queue is empty, we have visited all nodes, so return the visited nodes.
    if (queue.isEmpty()) {
      return Array.from(visited);
    }

    // Get the next node to visit from the queue.
    const node = queue.dequeue();

    // Visit each neighbor that hasn't been visited before.
    graph[node].forEach((neighbor) => {
      if (!visited.has(neighbor)) {
        visited.add(neighbor);
        queue.enqueue(neighbor);
      }
    });

    // Recursively call traverse to visit the next node in the queue.
    return traverse();
  }

  // Call traverse to start the traversal.
  return traverse();
}

Edge Cases

Empty graphs: Return an empty array without crashing.
Graphs with only one-two nodes: Traverse without crashing.
Cyclic graphs: Make sure not to traverse visited nodes again.
Disjoint graphs: Doesn't require special handling but good to be aware of.

Time Complexity

In the worst case, BFS visits every vertex and every edge of the graph once. Therefore, the time complexity of BFS is O(V + E), where V is the number of vertices in the graph and E is the number of edges. This is because BFS has to explore all vertices and edges to ensure that it covers the entire graph.

Take note that you should not use Array.shift() as it takes O(n) time to dequeue, where n is the number of elements in the array.

Space Complexity

BFS uses a queue to keep track of the nodes to be visited. At any given time, the queue contains the nodes that are at the current level of the graph being explored. Therefore, the space complexity of BFS is O(maximum number of nodes in any level of the graph).

Breadth-first Search

Examples

Recap (Hint)

Breadth-first Search

Examples

Recap (Hint)

Similar Questions

Clarification Questions

Iterative solution

Recursive solution

Edge Cases

Time Complexity

Space Complexity

You must be signed in to view your submissions

Loading editor

Loading editor

Loading tests

JavaScript Console

Loading tests